With the advent of newer and faster video cards, real time Ray Tracing is the hype.
Although Ray Tracing has been used in the Visuals Industry (Cinematography, architecture, design) for many years, it hasn't been used in games for performance reasons. The number of calculations needed to render an image exceeds the time constrains games require.
So, what's Ray Tracing? Wikipedia provides a very good introduction to the subject [wiki]

The first step in Ray tracing, is finding where each ray (from the pixel position on the screen) will intersect an object.
We will do it in a simple way by checking whether each pixel falls within the circle radius. It's achieved by measuring the distance from the center of the circle to the pixel. If this position is smaller than the circle radius, then the pixel is drawn:
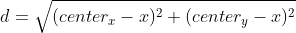
To reduce the number of calculations required, we used the squared distance (square roots can be expensive)
with the expected result:

First of all, we are considering that our rays are perpendicular to the screen (imagine they pass through the screen in direction to the wall)
These rays are defined as line segments, with a starting point Po (x, y, 0) and end point P1(x, y, depth). If this segment intersects the sphere, a pixel is drawn.
I will not go into the details of how the intersection between line segments and spheres is calculated. Please refer to this good source [AmBrSoft]
The following code uses those equations to find the intersection and draw a pixel:
Results can be seen in the following screenshot

Not surprised? It looks exactly like the previous image. Although that's true, what you are seeing here is a sphere, but it's equally lit (trust me).
Adding a light require us to know three things:
If you followed the link I provided, you can get the intersection point by finding the parametrized value t.
 As you can see, this equation may have 2 possible values. the smallest t will represent the closest intersection to the screen. We will choose that one.Finally, replace "t" in the parameterized line segment function.
As you can see, this equation may have 2 possible values. the smallest t will represent the closest intersection to the screen. We will choose that one.Finally, replace "t" in the parameterized line segment function.
(Note this code goes before drawing the pixel in the previous snippet)
The light component we are interested in is the diffuse light. Diffuse light is scattered by the object's surface when photons from the source light hit it. In a simplified model, we will calculate the diffuse light by measuring the angle between the light source and the Normal to the intersection on the sphere.
We do this by calculating the Dot product between the light source Normal, and the intersection Normal.
Finally we multiply the result of the dot product by the color, giving us different shades of yellow depending on the position of the light
(Calculating Intersection Normal)
(Calculating diffuse color based on Intersection normal and Light Normal)
Although Ray Tracing has been used in the Visuals Industry (Cinematography, architecture, design) for many years, it hasn't been used in games for performance reasons. The number of calculations needed to render an image exceeds the time constrains games require.
So, what's Ray Tracing? Wikipedia provides a very good introduction to the subject [wiki]
... rendering technique for generating an image by tracing the path of light as pixels in an image plane and simulating the effects of its encounters with virtual objects ...
The purpose of this post is to create the simplest 3D Ray Tracer I can think of.
This means that there are several constrains we will follow:
- Orthogonal Projection: All rays are cast parallel to each other
- Sphere: For simplicity, a sphere requires relatively simple math to calculate intersections and Normals
- Only one object will be rendered. This removes the need for calculations to determine if other objects block the light
- One Light source
- Diffuse light on the surface
- Render to Console (x64): Drawing in the console is pretty straightforward, as the purpose of this post is to demonstrate ray tracing
Drawing a Circumference
Having said that, let's warm up. What can be simpler than drawing a circumference?
A circumference can be parameterized in terms of it's radius, and an angle:
void DrawCircumference(HDC mydc) { COLORREF COLOR = RGB(255, 255, 0); for (double t = 0; t <= 2*PI; t += 0.01) { int x = static_cast<int>(RADIUS * cos(t)); int y = static_cast<int>(RADIUS * sin(t)); SetPixel(mydc, RESX/2 - x, RESY / 2 - y, COLOR); } }
The code above will draw a nice yellow circumference:

"Ray tracing" a circle
In this step, we are going to draw a filled circle in 2D. We won't exactly ray trace it, but in a similar way, we will go through each pixel in our window, and determine whether this pixel should be drawn or not.The first step in Ray tracing, is finding where each ray (from the pixel position on the screen) will intersect an object.
We will do it in a simple way by checking whether each pixel falls within the circle radius. It's achieved by measuring the distance from the center of the circle to the pixel. If this position is smaller than the circle radius, then the pixel is drawn:
To reduce the number of calculations required, we used the squared distance (square roots can be expensive)
void RayTraceCircle(HDC mydc) { COLORREF COLOR = RGB(255, 255, 0); Vec2 center(RESX / 2, RESY / 2); for (int x = 0; x < RESX; ++x) { for (int y = 0; y < RESY; ++y) { //Intersect circle? int distSq = (center.x - x) * (center.x - x) + (center.y - y) * (center.y - y); if (distSq < RADIUS * RADIUS) { SetPixel(mydc, x, y, COLOR); } } } }
with the expected result:
Ray tracing a Sphere
We are taking a leap now. Switching from 2D to 3D requires additional functionality in order to determine whether our rays intersect a sphere.First of all, we are considering that our rays are perpendicular to the screen (imagine they pass through the screen in direction to the wall)
These rays are defined as line segments, with a starting point Po (x, y, 0) and end point P1(x, y, depth). If this segment intersects the sphere, a pixel is drawn.
I will not go into the details of how the intersection between line segments and spheres is calculated. Please refer to this good source [AmBrSoft]
The following code uses those equations to find the intersection and draw a pixel:
void RayTraceSphere1(HDC mydc) { COLORREF COLOR = RGB(255, 255, 0); Vec3 center(RESX / 2, RESY / 2, DEPTH / 2); for (double x = 0; x < RESX; ++x) { for (double y = 0; y < RESY; ++y) { //parametrize Line Vec3 p0(x, y, 0); Vec3 p1(x, y, DEPTH); Vec3 v(p1.x - p0.x, p1.y - p0.y, p1.z - p0.z); Vec3 cp0(center.x - p0.x, center.y - p0.y, center.z - p0.z); //Calculate intersection double a = v.x * v.x + v.y * v.y + v.z * v.z; double b = -2 * ( v.x*cp0.x + v.y * cp0.y + v.z * cp0.z); double c = cp0.x * cp0.x + cp0.y * cp0.y + cp0.z * cp0.z - RADIUS * RADIUS; if ((b * b) < (4 * a * c)) { continue; } SetPixel(mydc, x, y, COLOR); } } }
Results can be seen in the following screenshot
Not surprised? It looks exactly like the previous image. Although that's true, what you are seeing here is a sphere, but it's equally lit (trust me).
Adding a light
The last step is to include a light source (so you can believe me it's a sphere)Adding a light require us to know three things:
- Line segment - sphere intersection
- Normal vector in the intersection
- Light position
If you followed the link I provided, you can get the intersection point by finding the parametrized value t.

(Note this code goes before drawing the pixel in the previous snippet)
double t0 = (-b - sqrt(b * b - 4 * a * c)) / (2 * a); double t1 = (-b + sqrt(b * b - 4 * a * c)) / (2 * a); double t = t0 < t1 ? t0 : t1; Vec3 intersect(p0.x + v.x * t, p0.y + v.y * t, p0.z + v.z * t);
The light component we are interested in is the diffuse light. Diffuse light is scattered by the object's surface when photons from the source light hit it. In a simplified model, we will calculate the diffuse light by measuring the angle between the light source and the Normal to the intersection on the sphere.
We do this by calculating the Dot product between the light source Normal, and the intersection Normal.
Finally we multiply the result of the dot product by the color, giving us different shades of yellow depending on the position of the light
(Calculating Intersection Normal)
Vec3 N(intersect.x - center.x, intersect.y - center.y, intersect.z - center.z); double Nsize = sqrt(N.x * N.x + N.y * N.y + N.z * N.z); N.x /= Nsize; N.y /= Nsize; N.z /= Nsize;
(Calculating diffuse color based on Intersection normal and Light Normal)
Vec3 CalculateDiffuse(Vec3 const& intersect, Vec3 const& normal, Vec3 objColor) { Vec3 Nlight(position.x - intersect.x, position.y - intersect.y, position.z - intersect.z); Nlight.Normalize(); double dot = dotP(normal, Nlight); dot = dot < 0 ? 0 : dot; objColor.x *= color.x; objColor.y *= color.y; objColor.z *= color.z; objColor.Mult(dot); return objColor; }
That's it, when executing the program, the result is a sphere lit by a light source:

Comments